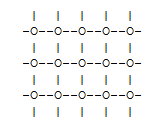
1 The Role of Models in Physics
The science of physics assumes that physical phenomena may be explained and understood as a result of the functioning of physically real systems structured in certain ways and constituted of elements possessing certain properties. The exact nature of the real system in itself is usually unknown, so to gain an understanding of it a model (whose exact nature is known) is constructed.An abstract model is a system (normally conceptual but possibly physical[2]) of parts and wholes which are held to interact in certain ways, described so as to be clear to any interested and competent observer, and to interact in such ways consistently over time (thereby allowing prediction as well as explanation). The model incorporates analogues of those aspects of the real system which are relevant to the phenomena to be explained.
Explanation is by analogy: the conceptual analogue of the physical phenomenon to be explained is understood as occurring as a result of the properties of the model, and the phenomenon itself is then explained as a result of assumed properties of the real system which are analogous to the properties of the model.[3]
Successful prediction based upon such understanding encourages us to believe that the model is true (although there is the possibility that future experience will reveal that we were mistaken in so believing).
This does not prove that the real system in fact has the structure and functioning attributed to it in the model. Generally we can never in any case know what the structure and functioning of the real system in itself is except by analogy with some model. To the degree in which the properties of the model are mirrored by the properties of the real system (its "adequacy") we are justified in believing that the model gives us knowledge of the constitution of the real system.
This is all fine so long as we don't have two different, equally adequate, models. Especially if the two models are not just "different" but "apparently irreconcilable". Unfortunately this may happen. A well-known instance of two such apparently irreconcilable models is the theory of light as consisting of waves and the theory of light as consisting of particles ("photons"). The wave model of light and the particle model of light each adequately explain certain observed phenomena. Yet cognitive dissonance may be felt if both models are accepted as true because conceptually waves and particles are very different things. Thus arises the problem of the real nature of light: does it consist of waves or of particles? Or both? Or neither?
2 Computational Physics
The research described in this study is part of the field of condensed matter physics, that branch of physics concerned with explaining how combinations of extremely large numbers of particles such as atoms or electrons behave in certain interesting ways under certain conditions. It is a science which seeks for laws describing the overall properties of systems in which many particles interact. This work is also in the field of statistical physics, which attempts to predict the properties of complex systems containing many interacting components undergoing random thermal motions.
Condensed matter physics (like other fields of physics) may be subdivided into three kinds: theoretical, experimental and computational.
(i) Experimental physics
This involves observers interacting directly with those aspects of physical reality which are under investigation. The practice of modern experimental physics is to set up one or a series of experiments designed to decide among one of (usually) many possible outcomes. The point of an experiment is that the outcome is not known in advance; rather it is Nature which decides the outcome and we observe.
(ii) Theoretical physics
Theoretical physics consists in the formulation and testing of theories about the structure and functioning of systems believed or supposed to be present in physical reality. Such theories often make use of conceptual models (as described above). Part of the model may consist in the assertion that certain aspects of the model may be described mathematically and exhibit certain mathematical relations, thereby allowing properties of the model to be deduced on the basis of results established by mathematicians. If these deduced properties are confirmed by experiment then we have reason to trust the model.
(iii) Computational physics
This is a branch of physics distinct from the other two because (a) unlike experimental physics it does not query Nature directly and (b) unlike theoretical physics its results are not arrived at primarily by theorizing but rather by computation.
Most results arrived at in computational physics are not statements that could ever be logically derived from a description of the model. E.g., values of the so-called critical temperature, critical exponents, etc., in a spin model of magnetic material. So the computational experiment typically does not just reveal what could have been deduced (were it not for complexity and mass of data) by theorizing.[4]
There are, however, some exceptions to this, notably, the analytical solution of the 2-dimensional Ising model on a square lattice by Lars Onsager in 1944, which provides, e.g., the exact value of the critical temperature. For other models no analytic solution has been found except by the imposition of assumptions which simplify the mathematical description so that it becomes amenable to currently existing mathematical techniques.
Given that the construction and querying of computational models is the main activity of a computational physicist, what distinguishes him from a simple computer programmer? Given that a certain computer model may have a certain plausibility and elegance, what saves a computational physicist from becoming captured by his model, so to speak? Computational physics is not a science of the properties of selected computer models, however interesting they may be to study. Such a science, though it might be a part of the science of computational physics, would be in itself a branch of computer science, not a branch of physics.
Computational physics, like the other branches of physics, aims at knowledge of the physical world. It arrives at this knowledge by showing that a model has the same properties (within limits of uncertainty in measurement), as revealed by computation, as the system modelled, as revealed by direct querying of Nature (the province of the experimental physicist).
Insofar as a model incorporates theoretical hypotheses, and facilitates predictions, this process provides a test of the theory. Thus there is a synergistic relationship among the three branches of physics, the experimental, the theoretical and the computational.
Finally we may consider the claim that computational physics is really just the handmaiden of theoretical physics, not a distinct branch of physical science, on the grounds that the computational physicist simply obtains results which are implicit in the theoretical model (upon which the computer model is based), results which the theoretical physicist cannot himself obtain because of the complexity of the model and the large amount of computation needed.
But most results arrived at by the computational physicist are not, even in principle, capable of being derived by logical deduction from a description of the model — at least not in the case of Monte Carlo experiments. These are experiments (and the principal kind of experiment conducted by computational physicists) which depend upon a stream of many random numbers. E.g., we have a spin system which is a model of magnetic material[5], in which the spins are either up or down and the system evolves over time according to certain rules involving "chance". Each spin is considered for possible flipping about as often as any other spin, and it flips or it doesn't flip according to a criterion which involves the generation of a random number. Since the random numbers, although generated by a deterministic algorithm, behave as true random numbers (if the algorithm is properly designed), they cannot be predicted, so whether a given spin at a given time will flip or not flip is completely unpredictable.[6]
The system is allowed to evolve over time according to this dynamics, and when the system attains equilibrium certain measurements are made, e.g., the analogues in the model of magnetization, specific heat, etc. By considering a range of temperatures (or conducting other such computational experiments) we find out how these properties depend on temperature or other factors. But the measurements, and so the properties of the system, are not, even in principle, deducible from the theoretical description of the system and the rules for its evolution. Therefore the computational physicist can arrive at results which the theoretical physicist cannot arrive at. Thus computational physics cannot be characterized simply as theoretical physics aided by computing power, and so is a branch of physics distinct both from the experimental and the theoretical.
3 Modelling Magnetic Material
Magnetism (or electromagnetism) is one of the fundamental forces of Nature. A field of magnetic force is produced by the motion of an electrically charged particle, and so an electric current (which consists of moving electrons) produces a magnetic field.
In 1925 G. E. Uhlenbeck and S. Goudsmit[7] hypothesized that the electron has a "spin", and so behaves like a small bar magnet, and that in an external magnetic field the direction of the electron's magnetic field is either parallel or antiparallel to that of the external field.
In the same year Lenz suggested to his student Ising [1900-1998] that if an interaction was introduced between spins so that parallel spins in a crystalline lattice attracted one another, and antiparallel spins repelled one another, then at sufficiently low temperatures the spins would all be aligned[8], and the model might provide an atomic description of ferromagnetism. (Domb 1974, pp.357-358)
Thus arose the "Ising model" in which "spins", located on the sites of a regular lattice, have one of two values, +1 and –1, and spins with spin values Si and Sj on adjacent sites interact with an energy –J.Si.Sj (where J is a positive real number[9]), so that spins with similar values interact with an energy -J, and those with dissimilar values interact with the (higher) energy J (the whole system tending toward a state of lower energy, unless energy is added from outside, e.g. by means of a "heat bath"). The magnetization per spin of a system of N spins is defined as Σi(Si / N) (which thus lies between –1 and +1) and the total energy (the "Hamiltonian") is defined as the sum of the interaction energies, i.e.,
Σij(-J.Si.Sj) = –J.Σij(Si.Sj)
where the sum is over all pairs of nearest neighbour spins.[10]
If the spins are allowed to have more than two states we have the "Potts model", named after the Australian mathematician R. B. Potts who published a study of this model in 1952.[11]
Magnetic materials exhibit interesting temperature-dependent behaviour. In particular, above a certain temperature (characteristic of the particular material) any magnetization present disappears. When the temperature is reduced below that temperature regions of stable magnetization spontaneously appear (even in the absence of an external magnetic field). This temperature is called the "critical" or "Curie" temperature. Various discontinuities (called "phase transitions") in measurable properties are found to occur at the critical temperature.[12]
The criterion with which to test the model is whether it gives rise to the characteristic pattern of singularities associated with ferromagnetism, and more particularly whether a Curie temperature, Tc, can be defined with the property that there exists a non-zero spontaneous magnetization for T < Tc. (Domb 1974, p.358)
Ising studied the simplest possible model consisting simply of a linear chain of spins, and showed that for this 1-dimensional case there is no (non-zero) critical temperature (i.e., the spins become aligned only at T = 0).
Ten years elapsed before Peierls showed that the two-dimensional model does have a non-zero spontaneous magnetization, and can therefore be regarded as a valid model of a ferromagnet. (Domb 1974, p.358)
In 1944 the physicist Lars Onsager, studying the 2-dimensional Ising model on a square lattice, was able to demonstrate by analytical means the existence of a phase transition in the model, a result considered to be a landmark in the physics of critical phenomena.[13]
In the mid-20th Century it became possible to use high-speed electronic computers to set up models of magnetic materials, to study the corresponding behaviour of those models, and to compare the computational results with observations of real systems. In recent years there have been many computational studies of the behaviour of magnetic materials at the critical temperature using Ising and Potts spin models. These studies often use so-called "Monte Carlo" techniques (described in Hammersley and Handscomb 1964), which are methods relying on a stream of random numbers to drive a stochastic process, in this case the generation of a succession of many states of the spin model (as is the case in this research). The course of this process is governed by the choice of a "dynamics algorithm", a concept which will be explained below.
We now turn to a detailed discussion of the ways in which the Ising and Potts models are implemented for the purpose of simulating the behaviour of ferromagnetic material.
First the concept of a lattice geometry is discussed, then precise definitions of the Ising and the Potts spin models are given. We then consider how temperature enters the model, and how the model is made to evolve over time (by means of one or another algorithm controlling the dynamics). Further related issues are discussed, such as the fact that we use finite models in an attempt to gain knowledge of the behavior of the ideal infinite system.
In a system of spins the spins must have some location, or at least there must be some way to relate them to each other and to decide which of them interact (usually only "nearest neighbour" spins interact). This may be done by postulating a regular geometric "lattice" structure consisting of lines joining vertices. A simple example of a lattice geometry is the "square" lattice:
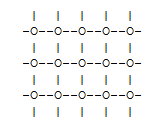
The analogue of this in three dimensions is the "cubic" lattice, and 4- and higher-dimensional analogues are known as "hypercubic" lattices.
Other geometries which have been used in spin models are the "honeycomb" lattice:
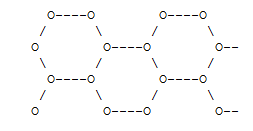
the "triangular" lattice:

and the 3-dimensional lattice known as the "diamond lattice", which is the structure of the carbon atoms in a diamond crystal.
A vertex in the lattice which may be occupied by a spin is known as a "site". Thus spins occupy the sites of a lattice, but not every site must be occupied by a spin. A line joining two sites is called a "lattice bond".
One of the characteristic properties of a lattice geometry is the number of sites directly connected to a site. This is usually the same for all sites. If it is then that number is known as the coordination number of the lattice.[14]
The coordination numbers of various possible lattice geometries are given below:
| Dimensionality | Name | Coordination number |
| 2 | honeycomb | 3 |
| 2 | square | 4 |
| 2 | triangular | 6 |
| 3 | diamond | 4 |
| 3 | cubic | 6 |
| 3 | tetrahedral | 12 |
| 4 | hypercubic | 8 |
More complex lattice structures are, of course, possible, but in computational physics they are seldom studied because they have not been found to occur in real physical systems.
In most studies a spin system includes a lattice in which all sites are occupied by spins and in which all lattice bonds are interpreted as energetic bonds (i.e., associated with that bond is an energy which contributes to the total energy of the system). Such a lattice (or spin system) is called a "pure" or "non-diluted" lattice.
In some recent studies (and in this research) not all lattice sites must be occupied by spins and not all lattice bonds are energetic bonds. In a site-diluted lattice not all lattice sites are occupied by spins. In a bond-diluted lattice not all lattice bonds are energetic bonds.
In the case of a bond-diluted lattice we may distinguish between lattice bonds which are open, meaning that the spins connected interact energetically, and those which are closed, meaning that the spins connected by such lattice bonds do not interact energetically, so in a bond-diluted lattice there is a mixture of open bonds and closed bonds.
It would also be possible to consider both kinds of dilution simultaneously, whereby not all lattice sites are occupied and not all spins on neighbouring sites are connected by an open bond. So far there seem to have been no studies published of this form of dilution.
5 Ising and Potts Spin Models
A spin systemconsists of:
(a) A "lattice", being a non-empty set, whose elements are called "lattice sites", and a binary, irreflexive, symmetric relation (of "bonds") among those sites.[15]
(b) A non-empty subset of lattice sites, said to be "occupied"; each such lattice site is occupied by a single "spin".
(c) A non-empty subset of the set of lattice bonds connecting occupied sites; such bonds are said to be "energetic" bonds (a.k.a. "open" bonds).
(d) A set of real numbers, interpreted as "spin values"; each spin possesses a single spin value (which may change).
(e) A definition of the interaction energy between any two spins in terms of their spin values.[16]
(f) A definition of the total energy of the spin system (the "Hamiltonian") in terms of these interaction energies (and thus ultimately in terms of the spin values of the spins).
As stated in Section 4, a spin system in which all sites are occupied by spins, and all bonds are open, is said to be "pure". A spin system with some sites not occupied by spins is said to be "site-diluted". A spin system with some spins directly connected by closed lattice bonds is said to be "bond-diluted".
Two lattice sites which are directly connected by a lattice bond are said to be "nearest neighbour" lattice sites. Two spins on sites directly connected by an open lattice bond are said to be "nearest neighbour" spins. In a bond-diluted lattice it is possible for two spins to occupy nearest neighbour lattice sites even though those spins are not nearest-neighbour spins (in the case that they are connected by a closed lattice bond), e.g., spins a and b in the following lattice (where open bonds are marked by — and|, and closed bonds by ....):
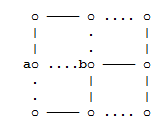
A spin system is said to be a "nearest neighbour" spin system if the interaction energy between any two spins which are not nearest neighbour spins is zero. All spin systems studied in this research are nearest neighbour spin systems.
A "state" of a spin system is a mapping of each spin to a spin value.[17]
The standard Ising spin model is a spin model (on some lattice), such that:
(a) The set of spin values is { +1, -1 }.
(b) The value of the interaction energy associated with any pair of nearest neightbour spins Si and Sj is –J.Si.Sj, where J is a non-zero real number.
(c) The Hamiltonian (assuming the absence of any external magnetic field) is the sum of the interaction energies over all pairs of nearest neighbour spins (only), i.e., -J.Σij(Si.Sj).
For a model of a ferromagnetic material J > 0, and for a model of an antiferromagnetic material J < 0. This research concerns only models of ferromagnetic material.
The standard q-state Potts spin model is a spin model in which there can be q different spin values, with q ≥ 2. The spin values are normally denoted by the numerals 1, 2, …, q.
There are two variants of the q-state Potts model, depending on how the interaction energy is defined.
The q-state Potts spin model, Version A, is a spin model, as defined above, such that the interaction energy associated with any pair of spin values Si and Sj is –J.δ(Si,Sj), where δ() is the Kronecker delta function: δ(x,y) = 1 if and only if x = y (otherwise 0).
The q-state Potts spin model, Version B, is a spin model such that the interaction energy associated with any pair of spin values Si and Sj is
–J.[2.δ(Si,Sj)-1]
In both versions, as in the Ising model, the Hamiltonian is the sum of the interaction energies over all nearest neighbour spins (assuming the absence of any external magnetic field).
The critical properties (other than the critical temperature) of these two versions of the q-state Potts model are the same.
6 Dynamics and the Principle of Detailed Balance
All physical systems undergo change. The definition of a spin model in Section 5 allows for change in the values of the spins, and we now consider this aspect of the model more closely.
Given a particular spin system (e.g., an Ising spin system on a square lattice of size 10x10) we may speak of the phase space of that system, which is the set of all possible assignments of spin values (+1 or -1) to the spins. Clearly in this example there are 2100 (c. 1030) states in the phase space.
It might be thought that we could measure a quantity such as magnetization by random sampling of the phase space, i.e., by sampling many states at random, calculating the magnetization and averaging them. But there are two objections to this:
(i) In a physical system (at a certain temperature) some states are far more (or less) likely than others. At higher temperature states which are disordered are far more likely than states which are ordered (i.e., which have regions of aligned spins). A random sampling of states (or more exactly, a sampling of states by randomly assigning spin values to the spins) will strongly favour disordered states, with magnetization close to zero (where magnetization is defined as usual as M = (ΣiSi)/N, where N is the number of spins and each spin Si has spin value +1 or -1) .
(ii) In any case, so far there is no analogue of temperature in our definition of a spin model. The magnetization of a physical system clearly depends on the temperature, and random sampling of the phase space takes no account of the possibility of magnetization being dependent on temperature.
An important concept in thermodynamics is that of thermal equilibrium. A system at thermal equilibrium exhibits no tendency to change its bulk properties — its extensive properties such as mass or its intensive properties such as magnetization and temperature.[19]
To obtain a realistic measurement of a quantity such as magnetization we need to sample the phase space in such a way that the probability of selecting a state is the same as (or very close to) the probability of that state occurring when the system is in equilibrium. Then the values of the quantities for the states sampled contribute to the average in just the degree that those values occur in the real system.
Now (according to thermodynamic theory) the probability P(X) of a system at thermodynamic equilibrium being in state X is e(-βEx) / Z where β = 1/(kBT), with T the temperature and kB the Boltzmann constant, 1.380658 x 10-23 J/K (Wildi, 1991, p.49), Ex is the energy of state X and Z is the partition function, Z = ΣYe(-βEY), where the summation is over all possible states Y (with energy denoted by EY) of the system.[20] In the case of a spin model Ex is the Hamiltonian, as mentioned in the definition of a spin model in Section 5.
But how to sample the phase space so that each state occurs with the same probability as its equilibrium probability?
The analogue in the model of the temporal evolution of a real magnetic system is a sequence of states (with some kind of connection between successive states). Such a sequence of states is called a trajectory through the phase space.
If a spin system starts in some initial state and is allowed to evolve according to some algorithm which generates a successor state from any given state (a dynamics algorithm) then we may measure the values of quantities such as magnetization, absolute magnetization, the second moment of the magnetization, etc., as the system evolves.
When the spin system has evolved to the point where the quantities of interest (magnetization, etc.) are stable, the system is in equilibrium. We can then measure the equilibrium properties of the system by taking an average of quantities measured at each state over a sequence of states sufficient in number to give us a reasonable measurement of mean and standard deviation. This is called a time average of a quantity.
Combining a dynamics algorithm (for producing a sequence of states) with a spin model allows us to obtain trajectories through the phase space. This dynamic evolution may occur either as a result of a succession of single spins changing their value ("single spin flip" or "local" dynamics) or as a result of groups of connected spins changing their values together ("cluster flip dynamics").[21]
However, a priori, we have no assurance that the dynamics algorithm used will actually produce (eventually) a stable equilibrium condition. How can we find a dynamics algorithm which is guaranteed to produce an equilibrium condition (thereby allowing us to measure the equilibrium properties of the system)?
Suppose a spin system evolves as described above, and suppose that we have a dynamics algorithm such that for any given state A there is a definite probability that it will be succeeded in the trajectory by state B (for any possible state B), and let P(A→B) denote that probability (called a transition probability).
Let P(A,t) denote the probability that the spin system is in state A at time t. Then the rate of change of P(A,t) with respect to t is given by
ΣB[P(B,t).P(B→A)] - ΣB[P(A,t).P(A→B)]
i.e., the sum, over all states B, of the probability that the system is in state B ( ≠ A) at time t and moves to state A minus the sum, over all states B ( ≠ A), of the probability that the system is in state A at time t and moves to state B.
At equilibrium the rate of change of P(A,t) is zero (if it were not then some macroscopic property of the system would be changing, and so the system would not be in equilibrium). Thus we can speak of P(A), the equilibrium probability of state A (i.e., the probability, once the system has reached equilibrium, that it is in state A).
Thus for any time t at equilibrium, for any state A
ΣB[P(B,t).P(B→A)] = ΣB[P(A,t).P(A→B)]
where the summation is over all states B ≠ A. Thus at equilibrium for any state A
ΣB[P(B).P(B→A)] = ΣB[P(A).P(A→B)]
where the summation is over all states B ≠ A. Then
ΣB[P(B).P(B→A)] + P(A).P(A→A) = ΣB[P(A).P(A→B)] + P(A).P(A→A)
so we may drop the restriction in the summation that B ≠ A and thus at equilibrium for all states A
ΣB[P(B).P(B→A)] = ΣB[P(A).P(A→B)]
where the summation is over all states B.
This suggests what is called the principle of microscopic reversibility, a.k.a. the principle of detailed balance, which asserts that at thermodynamic equilibrium the likelihood of a system being in any state A and changing to any other state B is equal to the likelihood of its being in state B and changing to state A. This principle may be stated as:
P(A).P(A → B) = P(B).P(B → A)
for all states A and B.
In a landmark paper Metropolis et al. (1953) showed that if a dynamics algorithm, which is such that P(X → Y) is well-defined for any states X and Y, satisfies the principle of detailed balance then in the long run (in any trajectory) the probability of any state X occurring will be the same as its equilibrium probability e(-βEx) / Z.[22]
In the next section and in Section 9 we discuss dynamics algorithms which satisfy the principle of detailed balance, and so are suitable candidates for use in spin models of magnetic material.
7 Single Spin Flip Dynamics Algorithms
Dynamics algorithms used in spin model studies may be divided into single spin flip algorithms and cluster flip algorithms. Among the former are the so-called Metropolis algorithm and the Glauber (or "heat bath") algorithm. Among the latter are the Swendsen-Wang algorithm and the Wolff algorithm (discussed in Section 9).
In a single spin flip algorithm a spin is selected (in such a way that in the long run each spin is selected about as often as any other spin[23]) and a decision is then made as to whether it should take on a new spin value.
We then calculate the change in the energy of the system that would result if the spin changed its spin value to some other, and from this we calculate a so-called transition probability. This is such that the larger is the energy increase which would result from the spin flip the smaller is the probability that the spin will be flipped (the transition probability). We then choose a random number between 0 and 1. If this is less than the transition probability then the spin adopts the new spin value, otherwise the spin remains unchanged.
The change in the energy (from before the spin flip to after) can be calculated from the static properties of the spin system. The dynamics of the system is governed by the manner in which the transition probability is calculated, given this change in energy. This is done in different ways by these two dynamics algorithms, and the calculation depends upon a parameter T, which is the analogue of temperature.
Suppose a spin is in state Si and it is under consideration for change to state Sj and let the transition probability be denoted by P(Si → Sj). According to the principle of detailed balance (Section 6) we must have:
P(Si).P(Si → Sj) = P(Sj).P(Sj → Si)
that is,
P(Si → Sj) / P(Sj → Si) = P(Sj) / P(Si)
As noted in Section 6 the probability P(X) of a system at thermodynamic equilibrium being in state X is e(-βEx) / Z where β = 1/(kBT) and Z is the partition function. For the standard Ising model, as stated in Section 5, EX is -J.Σij(Si.Sj) for a state X with spin values Si = +1 or -1 for all spins Si.
Thus for any two states X and Y,
P(X) / P(Y) = [e(-βEx)/Z] / [e(-βEY)/Z] = e(-βEx) / e(-βEY) = e[-β(Ex-EY)] = e-βΔE
where ΔE = EX – EY is the change in energy of the system when it moves to state X from state Y. Thus a single spin flip dynamics algorithm satisfies detailed balance if and only if
P(Si → Sj) / P(Sj → Si) = e-βΔEji
where Si (resp. Sj) is the state of the system with the spin under consideration having spin value Si (resp. Sj), and ΔEji is the energy change resulting from the spin's changing from value Si to Sj.[24]
In order to calculate ΔEji it is not necessary to calculate the total energies of the "before" and "after" states. If ΔEji is the energy difference produced by changing the spin value of a single spin (as in the Metropolis and the Glauber algorithms) then ΔEji can be calculated by considering the sum of the interaction energies of that spin with its nearest neighbours before and after the contemplated change. This matter is treated in more detail in the author's "Calculation of the Metropolis and the Glauber Transition Probabilities for the Ising Model and for the q-state Potts Model".[18]
The transition probabilities (i.e., the likelihood that a spin will change its value) for the Metropolis algorithm and for the Glauber algorithm are defined as follows:
| Metropolis algorithm: P(Si → Sj) | = 1 if ΔEji ≤ 0 |
| = e-ΔEji/(kBT) otherwise. | |
| Glauber algorithm: P(Si → Sj) | = 1 / [ 1 + e ΔEji/(kBT) ] |
It is not difficult to prove that in both cases P(Si → Sj) / P(Sj → Si) = e-βΔEji, so both the Metropolis and the Glauber algorithms satisfy the condition of detailed balance.
In practice, when considering whether to flip a spin, one compares the value of the transition probability P(Si → Sj), as defined above, with a random number between 0 and 1, and flips the spin if and only if it is less than the transition probability. The transition probability is calculated from the energy difference, ΔEji. This value is arrived at on the basis of part (e) of the definition of the spin model (see Section 5), i.e., the definition of the interaction energy between any two spins in terms of their spin values. This interaction energy is defined in terms of the value of a spin and the value of its nearest neighbours (assuming a nearest neighbour spin model).
Since (in an Ising or a Potts spin model) the number of possible spin values is finite, the number of possible values of the interaction energies, -J.Si.Sj, is also finite. Since the number of nearest neighbours is finite, the number of possible values for ΔEji is also finite, and so there are only a finite number of possible transition probability values. Thus a table of transition probabilities can be constructed for any given spin model.
8 Temperature
The behaviour of real magnetic systems depends on temperature, so obviously there has to be some aspect of the model which corresponds to physical temperature.
In physics energy is any measurable quantity with dimension mass.length2/time2 (e.g., kinetic energy = ½mv2 for an object of mass m moving with speed v). In molecular dynamics, temperature is given by the average translational molecular kinetic energy of the molecules. In thermodynamics, temperature is the integrating factor of the differential equation referred to as the first law of thermodynamics, du = cvdT for a perfect gas, where du is the internal energy proportional to the temperature change, cv is the specific heat at constant volume and T is the Kelvin temperature.
However in the definition of a spin model in Section 5 there is nothing corresponding to the physical property of temperature. But we do have a quantity of energy, namely, the interaction energy between spins, denoted by J. It is convenient to assign to J the value 1.380658 x 10-23 joules, since this is the same numerical value as Boltzmann’s constant, kB = 1.380658 x 10-23 J/K, implying that J/kB = 1 (this ratio has units of degrees Kelvin).
Temperature enters when we consider the dynamics of a spin system, specifically, when we consider (as in the previous section) the probability that a spin will change its spin value. The parameter T which enters these calculations is the analogue of temperature. The units of ΔEji are joules, the units of kB are joules per degree Kelvin, and the units of T are degrees K, so the quantity ΔEji/(kBT) is dimensionless, as it should be if it is to be used as an exponent of e in the definitions of P(Si → Sj) in the previous section.
9 Cluster Flip Dynamics Algorithms
The Metropolis and the Glauber algorithms may (or may not) be close to reality in the way they represent the dynamics of real systems, but in computer simulations they are slow to achieve a condition of equilibrium when the temperature is close to the critical temperature. For this reason algorithms were developed which are more efficient (in the sense that equilibrium is attained more quickly).
(i) The Swendsen-Wang Algorithm
One of these is the Swendsen-Wang algorithm (Swendsen and Wang 1987), which is as follows: In a particular state of a spin system there are clusters of spins. A spin cluster consists of a set of spins, each of which is a nearest neighbour to at least one other spin in the cluster, with all spins having the same spin value. The Swendsen-Wang process consists of two parts: The first part is the creation of "virtual" spin clusters, as follows: If two spins are connected by an open lattice bond and those spins have the same value then a "virtual" bond is created between them with probability 1 – e-2/T, where T is the temperature. Thereby each spin cluster is partitioned into (smaller) virtual spin clusters. The second part of the Swendsen-Wang process is as follows: For each virtual spin cluster, select a spin value at random (from among all possible spin values) and assign that spin value to all spins in the virtual cluster.[25] This process is then repeated.
One application of this process results in each spin being considered for change once and once only, and so is equivalent to a single sweep through the lattice in the Metropolis and the Glauber algorithms.
(ii) The Wolff Algorithm
The Wolff algorithm (Wolff 1989) is as follows: A spin is chosen at random as the seed spin for the growth of a virtual spin cluster. The cluster is grown by adding spins as follows: For each spin added (starting with the seed spin) each of its nearest neighbour spin with the same spin value is added to the virtual cluster with a probability of 1 – e-2/T (the same as in the Swendsen-Wang algorithm). This process is repeated until no new spin is added. Then, in the case of Ising spins, all spins in the virtual cluster are flipped (to assume their opposite values), and in the case of the q-state Potts model all spins receive a spin value which is randomly chosen except that it is different from their current value. The process is then repeated.
Both the Swendsen-Wang algorithm and the Wolff algorithm can be shown to satisfy detailed balance (see Wang and Swendsen 1990 and Wolff 1989).
10 Time
A model of a physically real system must have an analogue of time. In the Metropolis, Glauber and Swendsen-Wang algorithms there is a natural unit of (analogous) time, namely, a single sweep through the lattice, during which each spin is considered once and once only for change.
For the Wolff algorithm the situation is less straightforward. We might take a cluster flip as a unit of time, but since the size of the Wolff cluster may vary over two orders of magnitude between low and high temperature, and the size of a Wolff cluster is inversely proportional to temperature, we would then have to say that many more spins are flipped per unit of time at low temperature than at high temperature, which is contrary to what we find in real systems.
An alternative approach to defining a unit of time for use with the Wolff algorithm is as follows: In a Swendsen-Wang time unit (assuming the Ising model) approximately half of the spins get flipped (since approximately half of the Swendsen-Wang clusters get flipped). Every Wolff cluster gets flipped, so in the Wolff process we can take as a time unit a sequence of a variable number of Wolff cluster flips such that the sum of the cluster sizes (which equals the number of spins flipped) equals (on average) one-half the number of spins. (At low temperatures most Wolff clusters are large, so we have to adjust continually the target number of Wolff clusters making up a time unit in order to maintain this relation between the number of spins flipped and the number of units of time elapsed.) Then the number of spin flips (on average) is the same in one unit of time for the Wolff algorithm as for the Swendsen-Wang algorithm.
For the q-state Potts model, in a Swendsen-Wang time unit approximately (q-1)/q of the spins get flipped, since for each virtual spin cluster the probability of the new spin value being different from the old is (q-1)/q. Every Wolff cluster gets flipped, so in the Wolff process with the q-state Potts model we can take as a time unit (similar to the above) a sequence of a variable number of Wolff cluster flips such that the sum of the cluster sizes equals (q-1)/q times the number of spins.
11 Boundary Conditions
Every computational model is finite, and no singularities or discontinuities are ever observed in a finite system. The discontinuities and singularities which are of interest in the study of critical phenomena occur only in ideal infinite systems, and cannot be observed in any model which can be realized physically (and thus not in a computer model).[26] The behaviour of actual models is only an approximation to ideal behaviour.
The difficulty of using a finite lattice to simulate an infinite lattice can be eased somewhat by the use of so-called periodic boundary conditions. We wish to embed the finite lattice in a virtual infinite lattice consisting of multiple copies of the finite lattice. This is accomplished by arranging for sites on one edge (or face, etc.) of the finite lattice to have as nearest neighbours sites on the opposite edge (or face, etc.), so that all sites have the same number of nearest neighbours whether or not they occur on an edge (or face) of the lattice. All simulations in this study are performed using periodic boundary conditions.
If sites on an edge (or face) have only the usual set of nearest neighbours (less in number than sites in the interior of the lattice) then the model is said to possess free boundary conditions.[27] Sometimes mixed boundary conditions are used, whereby the lattice "wraps around" only at some edges, e.g. to obtain (in the case of a square lattice) a cylindrical topology (compared to a toroidal topology in the case of periodic boundary conditions on a square lattice).
Other kinds of boundary condition are possible, such as the heliacal, obtained by taking a chain of sites and placing it on a helix so that n sites form one loop (thus creating a square lattice geometry), resulting in site m having as nearest neighbours sites n+m (above) and n-m (below).
12 Finite-Size Effects
As noted above, the discontinuities and singularities which are of interest in the study of critical phenomena occur only in ideal infinite systems. E.g., in the infinite square Ising model there is a discontinuity at Tc in the rate of change of magnetization M with respect to temperature T. For T > Tc, M=0, whereas for T < Tc there is a spontaneous non-zero magnetization. At Tc (moving from higher temperature to lower) there is a change from a constant zero M to an increasing M. But in a finite system the mean absolute value of M is non-zero even above Tc and there is no discontinuity in the rate of change at Tc. Only as the size of the model increases is there a better approximation to the ideal behaviour. Unfortunately larger systems require much longer computation time.
Estimates for various properties of the infinite system (such as critical exponents) may be made by assuming the validity of so-called finite-size scaling. Measurements of a quantity are made with a series of increasing lattice sizes, L1, L2, L3, ..., and the quantity is then plotted against the (decreasing) reciprocal of the size. If a linear fit to the data points is possible then we can extrapolate to zero to obtain an estimate of the value for a lattice of infinite size.[28]
It is important to note that in an infinite system the non-zero spontaneous magnetization is stable, but in a finite system it is "metastable", i.e., it will occasionally (due to unlikely sequences of spin flips mostly to the opposite of the dominant value) flip to the same value of opposite sign, where it stays for awhile before flipping back again.
Thus in spin model studies, with lattices of finite size, below Tc it is often advisable (especially when using cluster flip algorithms) to monitor the absolute value of the magnetization, rather than the magnetization itself, since if results are obtained by averaging (at each timepoint) over many runs the metastable positive magnetization and the metastable negative magnetization will average out to zero, and no non-zero stable magnetization will be observed.
1.This paper is Chapter 1 of the author's M.Phil. thesis (September 2000, University of Derby, U.K.), available at www.hermetic.ch/compsci/thesis/contents.htm
2. An example of a physical model is a model of a plane used in wind tunnel tests to investigate its aerodynamic properties.
3. Properties of the real system which are initially assumed to exist (by analogy with properties of the model) may subsequently be observed as a result of advances in techniques of observation, e.g. electron microscopy.
4. A fuller discussion of this point will be found in the next section.
5. The nature of such spin models is the subject of the following sections.
6. The (pseudo-)random number generator functions in the model as the analogue of randomness in Nature.
7. Uhlenbeck and Goudsmit 1925, as cited by Domb 1974.
8. It may be noted that in fact bar magnets free to rotate and placed next to each do not align themselves with their north poles in the same direction, but rather in opposite directions.
9. In this paper the following principle of italicisation is used: Where a mathematical expression occurs within a sentence it is italicised if and only if it consists of a single Roman character.
10. A more complicated model might allow energetic interactions between spins which are not nearest neighbours.
11. Renfrey Burnard Potts was Professor of Applied Mathematics, University of Adelaide, 1959-90.
12. A first-order phase transition is one in which a discontinuity occurs in a macroscopic quantity such as density, heat capacity, etc. as temperature or pressure is changed. It is the discontinuity that identifies the phase transition. In alloys and magnetic systems there are phase transitions that are second-order, meaning that the macroscopic properties do not change discontinuously at some particular temperature or pressure, but rather the rate of change of those quantities with respect to temperature or pressure does. Instead of jumping in value, a quantity suddenly goes from not changing to changing, or from changing at a certain rate to changing at a different rate. Examples are the magnetization of magnets and the crystal pattern of alloys, both of which are zero above a certain critical temperature and then start to increase below that temperature.
13. Prior to Onsager, Kramers and Wannier (1941) had made contributions to the solution of the problem.
14. The number of vertices to which a vertex in the lattice is directly connected by lines may be larger than the coordination number of the lattice. For example, it is possible to embed a honeycomb lattice (with coordination number of 3) in a square array of vertices, each of which is connected directly to four other vertices. In this case not all of the vertices are lattice sites (perhaps just half are).
15. In mathematics the term "lattice" is usually used in a more restricted sense, in which the binary relation is a partial ordering of a set satisfying certain conditions, and in which the set always contains a greatest and a least element with respect to this partial ordering.
16. In a spin model which is not a "nearest neighbour" spin model the interaction energy also depends on the distance between the spins (where "distance" means the length of the shortest connecting chain of spins).
17. In this report we shall often not distinguish notationally between a spin and its spin value in a given state, denoting both by terms such as Si.
18. See www.hermetic.ch/compsci/tranprob.htm.
19. This constancy at the macroscopic level does not imply constancy at the microscopic level, because at the level of atoms and electrons there is continual change. The spins of the electrons in a magnetic material are continually flipping, at a rate dependent on the temperature of the system, yet (if the system is in equilibrium) the overall magnetism remains constant (in the absence of outside influences).
20. For example, suppose a system consists of exactly two elements, each of which may have one of two energies, 0 or 1, then (assuming we can distinguish the two elements) there are four possible states of the system, one with energy 0, two with energy 1 and one with energy 2. Taking kB = 1 the partition function is Z = e0 + 2e-1/T + e-2/T. For T = 1, Z = 1.8711, and the probabilities of the system being in a certain state (at T = 1) are p(00) = 0.5344, p(01) = p(10) = 0.1966 and p(11) = 0.0723.
21. These two kinds of dynamics will be discussed further in the Sections 7 and 9.
22. A "plausibility argument" to show that this is so is given by Binder and Heermann (1998), pp.18-19.
23. Spins may be selected in various ways: (i) One may go through the lattice "typewriter fashion". (ii) One may select the spins randomly. (iii) One may divide the lattice into sublattices (similar to a checkerboard divided into squares) and select a spin from each sublattice in turn, going through the sublattices in typewriter fashion. (ii) is perhaps most realistic, but requires extra computing time to generate random numbers. In this study method (iii) is used in single spin flip dynamics.
24. The terms Si and Sj are here used to denote both the state of the spin system and the value of the spin under consideration.
25. Since the random spin value selection may produce the spin value already possessed by the spins of a virtual spin cluster not all virtual clusters are changed.
26. We can observe critical phenomena in physical reality, e.g. melting of solids, because the number of atoms involved is practically infinite.
27. It is interesting to note that work by Heermann and Stauffer (1980) suggests "that free edges approximate the infinite system as well as the more complicated periodic boundary conditions", at least in the case of the bond-diluted square lattice with lattice sizes from 10x10 to 240x240.
28. Suppose n sizes L0, ..., Ln-1 are such that the reciprocals 1/L0, ..., 1/Ln-1 are equally spaced in the interval [0,1/L0]. Then for all 0 ≤ i ≤ n we have 1/Li - 1/Li+1 = 1/L0.1/n. Thus 1/L0 - 1/L1 = 1/(n.L0) so 1/L1 = (1/L0).(1-1/n), and by induction 1/Li = (1/L0).(1-i/n). So Ln-1 = n.L0 so L0 = Ln-1/n. Thus the choice of n and either L0 or Ln-1 determines all the other sizes (or approximate sizes if the factors of n.L0 do not allow for whole number solutions). Taking n = 6 and Ln-1 = 60 implies sizes 10, 12, 15, 20, 30 and 60, with the intervals between the reciprocals of the sizes being 1/60. Taking n = 6 and Ln-1 = 180 implies sizes 30, 36, 45, 60, 90 and 180, with the intervals between the reciprocals of the sizes being 1/180.
29. For an explanation of the method of representing the lattice geometries mentioned in this work (and other lattice geometries) see the author's Lattice Geometries.
Domb, C., 1974, "Ising Model", in Domb, C., and Green, M.S., 1974, Phase Transitions and Critical Phenomena, Vol. 3, 357-484.
Hammersley, J.M., and Handscomb, D.C., 1964, Monte Carlo Methods, London: Methuen.
Heermann, D.W., and Stauffer, D., 1980, "Influence of Boundary Conditions on Square Bond Percolation near pc", Z. Phys. B, 40, 133-136.
Kramers, H.A., and Wannier, G.H., 1941, "Statistics of the two-dimensional ferromagnet, I and II", Phys. Rev., 60, 252-276.
Metropolis, N., Rosenbluth, A. W., et al., 1953, "Equation of State Calculations by Fast Computing Machines", J. Chem. Phys., 21, 1087-1092.
Meyer, P.J., "Computational Studies of Pure and Dilute Spin Models", on this site
Okano, K., Schülke, L., Yamagishi, K., and Zheng, B., 1997, "Universality and scaling in short-time critical dynamics", Nucl. Phys. B, 485, 727-746.
Onsager, L., 1944, "Crystal physics, I. A two-dimensional model with an order-disorder transition", Phys. Rev., 65, 117-149.
Stinchcombe, R., 1983, "Dilute Magnetism", in Domb, C., and Lebowitz, J. L., Phase Transitions and Critical Phenomena, Volume 7, Academic Press, 151-280.
Swendsen, R. H., and Wang, J.-S., 1987, "Nonuniversal Critical Dynamics in Monte Carlo Simulations", Phys. Rev. Lett., 58, 86-88.
Wildi, T., 1991, Units and Conversion Charts, New York: IEEE Press
Wolf, U., 1989, "Collective Monte Carlo Updating for Spin Systems", Phys. Rev. Lett., 62, 361-364.
| Home Page of this Hermetic Systems Website |
| Home Page of the other Hermetic Systems Website |