Chapter 4: Critical Temperatures of Dilute Ising Spin Models4.1 Thermal Equilibrium in Dilute Systems
The question of deciding when a spin system has reached equilibrium has been discussed in Section 3.2 in the context of pure spin systems. When we come to deal with dilute spin systems we cannot simply assume that a dilute system will equilibrate in the same time that a pure system will. As before, we need to conduct trials.
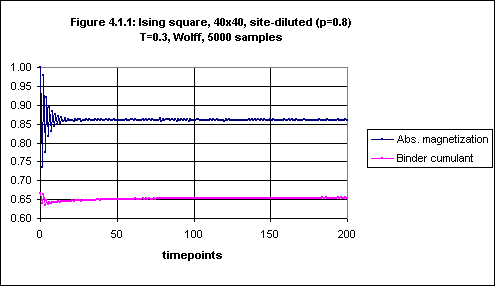
Figures 4.1.1 through 4.1.4 show results for an Ising square lattice, size 40x40, with site concentration 0.8 at the low temperature of 0.3 (which is about 20% of the critical temperature for this degree of site dilution) with Wolff dynamics. 5000 samples were used to obtain averages at each timepoint.
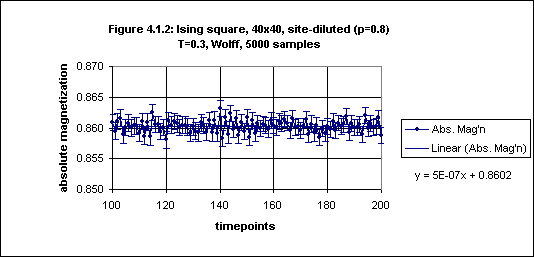
Figure 4.1.1 shows both the absolute magnetization and the Binder cumulant. It seems that the absolute magnetization is stable from timepoint 100 onwards, and this is confirmed by closer inspection of the plot for timepoints 100 through 200 as given in Figure 4.1.2.
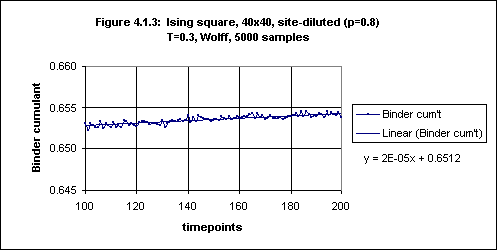
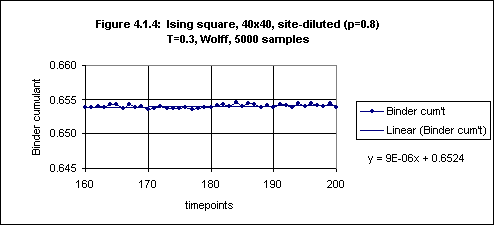
On the other hand, the Binder cumulant continues to rise, although very slowly, even after timepoint 100 (see Figure 4.1.3). However, from timepoint 160 onwards the increase is very small (see Figure 4.1.4). It thus seems that to obtain an equilibrium value for the Binder cumulant in this case we would be justified in averaging over timepoints 160 through 200.
For other values of the site concentration and the temperature similar trials were done to ascertain the earliest timepoint at which the magnetization and the Binder cumulant become stable.
4.2 A Critical Temperature of the Ising Cubic Lattice with Site Dilution
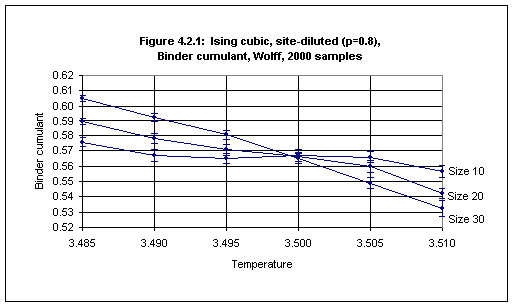
Using Wolff dynamics simulations were performed for the site-diluted cubic Ising model, with site concentration 0.8, on lattices of size 10, 20 and 30, for six temperatures, 3.485, 3.490, 3.495, 3.500, 3.505 and 3.510 (in each case 2000 samples were used), and the Binder cumulant was plotted against temperature (see Figure 4.2.1 and Table 4.2.1 in Appendix 5).1
There is slight overlap of the error bars for size 10 and size 20 at temperatures 3.495 and 3.505. If we ignore this then we may conclude that the critical temperature for the cubic lattice with site concentration 0.8 is 3.500(5). Otherwise we can conclude that the critical temperature is 3.500(10), i.e. 3.50(1).
Heuer (1993), using Monte Carlo methods, studied the cubic Ising model over a range of dilutions and obtained critical temperatures using the Binder cumulant method. For p = 0.8 he obtained a value of 3.4992(5), and says that his result "agrees very well with the critical temperature Tc(p = 0.8) = 3.4991(5) of Wang et al. [Wang 1991] who have determined Tc from the extrapolated susceptibility maximum."
Thus the result given by the simulation software provides confirmation of its validity not only for pure lattices but also for site-diluted lattices.
4.3 Dependence of Critical Temperature on Site Dilution in the Ising Square Lattice
The site percolation threshold is the lowest concentration of occupied sites in a lattice of a certain type (all of whose bonds are open) at which an infinite cluster of occupied sites appears (when the lattice sites are occupied with a certain concentration of sites), and below which all clusters of occupied sites are finite.2 This, of course, applies only to the ideal case of an infinite lattice. When estimating the site percolation threshold by experiment one necessarily uses finite lattices and looks for the concentration at which a percolating cluster of occupied sites first appears (i.e., a cluster of sites which extends from one side of the lattice to the opposite side). For the square lattice the site percolation threshold is 0.592746, a result deduced by Sykes and Essam (1963, 1964).3
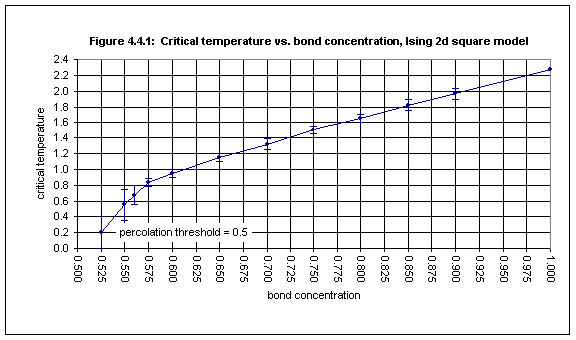
As the site concentration of a spin model on a lattice is decreased the critical temperature decreases. (This is because a smaller site concentration implies fewer connections among spins, thus it is easier for thermal fluctuations to overcome the tendency to long-range order.) In the ideal case the critical temperature becomes zero when the site concentration is decreased to the site percolation threshold.
The way in which the critical temperature of a spin model depends upon site concentration can be ascertained by measuring Tc for a series of site concentrations from the pure case (p=1.0) down to the percolation threshold. Critical temperatures may be measured using the Binder cumulant method as described in Section 3.1.
When measuring the critical temperature of a site-diluted lattice the main difference from the pure case is that averages must also be obtained over various configurations of occupied sites. In the pure case, since all sites are occupied, there is only one possible site configuration. When some sites are unoccupied there are many possible site configurations,4 and Monte Carlo studies of site-diluted lattices must also average over a random sampling of site configurations.
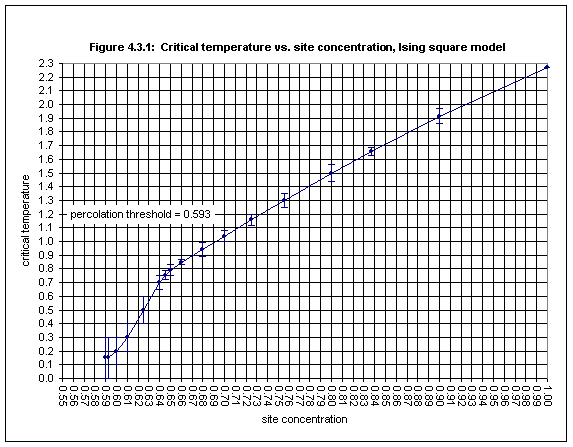
The results obtained for the square lattice are given in Table 4.3.1 and in Figure 4.3.1. The measurements of the Binder cumulant, from which the estimates of critical temperature are derived, are given in Table 4.3.5 in Appendix 5.
As the site concentration decreases it is necessary to average over a larger number of samples in order to reduce the size of the error bars. Whereas a few thousand samples is sufficient for small error bars in the case of site concentrations of 0.9 and above, for lower concentrations it may be necessary to average over as many as 100,000 samples to obtain acceptably small error bars, and for concentrations close to the percolation threshold even this may not be adequate, as Figure 4.3.1 shows.
Table 4.3.1
Determination of critical temperatures for a range of
site dilutions with the square Ising model.Site
oncentrationCritical
temperatureError
Number
of samples0.590
0.150
0.150
60,000
0.593
0.150
0.150
16,000
0.600
0.150
0.100
30,000
0.610
0.300
0.100
10,000
0.625
0.500
0.100
30,000
0.640
0.700
0.050
10,000
0.645
0.755
0.035
40,000
0.650
0.790
0.040
40,000
0.660
0.850
0.020
40,000
0.680
0.940
0.050
20,000
0.700
1.040
0.040
12,000
0.725
1.160
0.040
8,000
0.756
1.300
0.050
1,000
0.800
1.500
0.060
2,000
0.837
1.660
0.030
500
0.900
1.915
0.055
1,000
1.000
2.269
0.000
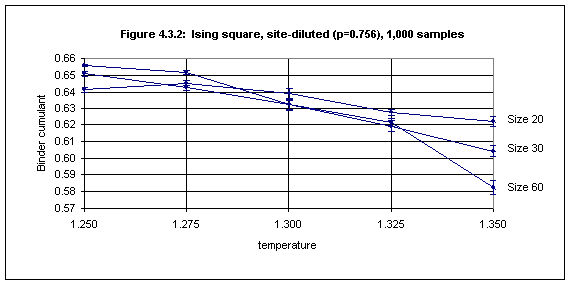
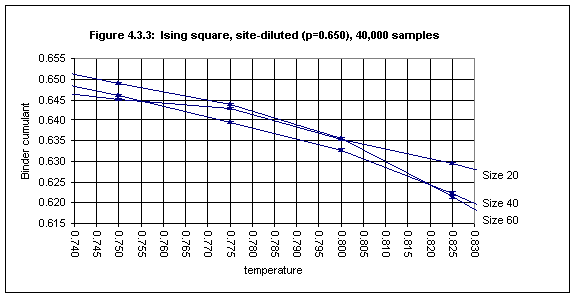
With the lattice sizes (20 - 60) and the number of samples (up to 60,000) used here the Binder cumulant method for determining Tc works well only for site-diluted lattices with site concentrations higher than about 0.65. Figures 4.3.2 and 4.3.3 show the plots for the Binder cumulant in the cases of p = 0.756 (1000 samples) and p = 0.65 (40,000 samples) respectively.
In Figure 4.3.2 non-overlapping of error bars occurs at temperatures 1.250 and 1.350 and we may estimate the critical temperature as 1.30(5).
In Figure 4.3.3 the error bars for T = 0.750 and T = 0.825 do not overlap (barely) and we may conclude that the critical temperature for site concentration 0.65 is 0.79(4).
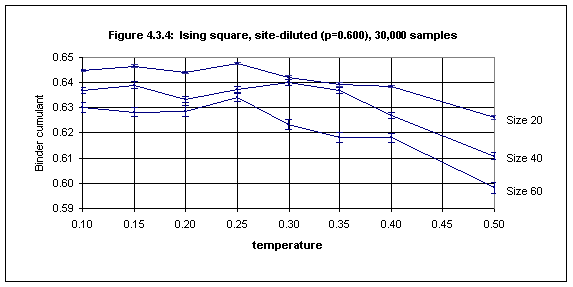
Below p = 0.65, however, it is hard to get good estimates. Figure 4.3.4 shows the Binder cumulant data for the case of p = 0.600 for the temperature range of 0.1 through 0.5 using 30,000 samples. There is little on which to base an estimate of Tc. Something like 0.2(1) is about the best one can do from this data.
In fact it appears that the Binder cumulant method for the determination of the critical temperature breaks down below a site concentration of about 0.65, because the plots for the Binder cumulant for different lattice sizes do not intersect as expected.
It could be that the expression for UL given in Section 3.1, UL = U[(T/Tc - 1).L1/ν], upon which the Binder cumulant method is based, is an oversimplification, and that some correction for strongly site-diluted lattices is required.
4.4 Dependence of Critical Temperature on Bond Dilution in the Ising Square Lattice
The bond percolation threshold is the lowest concentration of open bonds in a lattice of a certain type (all of whose sites are occupied) at which an infinite cluster of sites appears (when the bonds are opened with a certain concentration), and below which all clusters of sites are finite. This, of course, applies only to the ideal case of an infinite lattice. When estimating the bond percolation threshold by experiment one necessarily uses finite lattices and looks for the concentration at which a percolating cluster of sites first appears. For the square lattice the bond percolation threshold is exactly 0.5.
As with site concentration, as the bond concentration of a spin model is decreased, the critical temperature decreases. In the ideal case it becomes zero when the site concentration is decreased to the bond percolation threshold.
When measuring the critical temperature of a bond-diluted lattice the main difference from the pure case is that averages must also be obtained over various configurations of open bonds. In the pure case, since all bonds are open, there is only one possible bond configuration. When some bonds are closed there are many possible bond configurations,5 and Monte Carlo studies of bond-diluted lattices must average over a random sampling of bond configurations.
The results obtained for the square lattice are given in Table 4.4.1 and in Figure 4.4.1. The measurements of the Binder cumulant, from which the estimates of critical temperature are derived, are given in Table 4.4.2 in Appendix 5.
Table 4.4.1
Determination of critical temperatures for a range of
bond dilutions with the square Ising model.Bond
oncentrationCritical
temperatureError
Number
of samples0.525
0.200
0.200
200,000
0.550
0.550
0.200
128,000
0.560
0.675
0.125
200,000
0.575
0.830
0.050
100,000
0.600
0.950
0.050
64,000
0.650
1.150
0.050
32,000
0.700
1.320
0.070
16,000
0.750
1.500
0.050
8,000
0.800
1.650
0.050
4,000
0.850
1.820
0.070
2,000
0.900
1.970
0.070
1,000
1.000
2.269
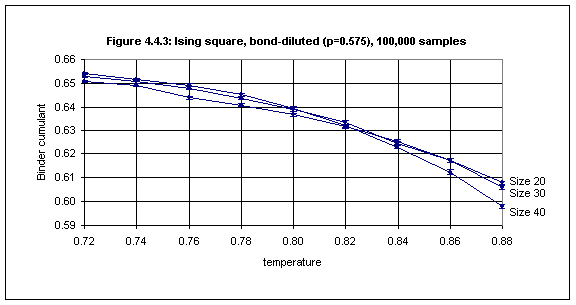
As the bond concentration decreases it is necessary to average over a larger number of samples in order to reduce the size of the error bars. Whereas a few thousand samples is sufficient for small error bars in the case of bond concentrations of 0.9 and above, for lower concentrations it may be necessary to average over as many as 100,000 samples to obtain acceptable error bars, e.g. for bond concentration 0.575 as shown in Figure 4.4.3.
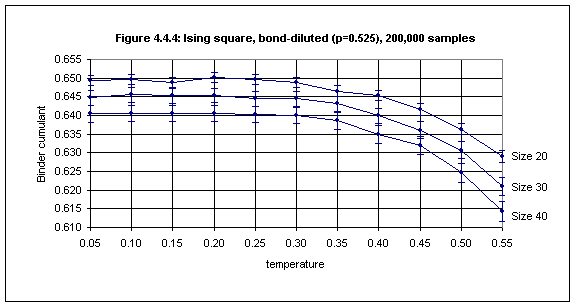
For bond concentrations lower than 0.55 (just above the bond percolation threshold of 0.5) it is difficult to obtain an estimate of the critical temperature, because the plots for lattice sizes 20, 30 and 40 do not intersect, as shown in Figure 4.4.4.
As in the case of site-dilution, it appears that the Binder cumulant method of determining critical temperatures breaks down as the bond concentration approaches the bond percolation threshold, because the plots do not intersect (despite the use of a large number of samples).
Title page Contents Next: Chapter 5 References